Sampling Curves with Finite Rate of Innovation
Hanjie Pan, Thierry Blu and Pier Luigi Dragotti

Introduction

We extend the theory of sampling and reconstructing signals with finite rate of innovation (FRI) to a specific class of two-dimensional curves, which are defined implicitly as the zeros of a mask funtion 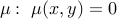. Here we approximate this mask function using a periodic Fourier expansion with few terms:

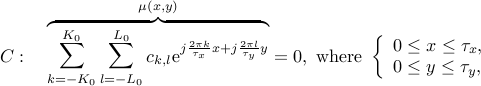
where 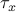and 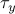are some positive real numbers that sepcify the 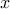- 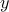dimensions of the rectangle that contains the curve. We can uniquely define 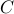within this rectangle with 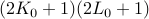coefficients 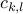, which are also known as “signal innovations” in the framework of finite rate of innovation (FRI). For each curve 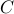defined on a 2D plane, we have an associated edge image:

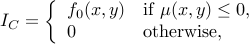
where 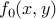is some analytic function. We can prove that the edge image 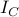associated with an FRI curve 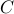satisfies a set of linear annihilation equations:

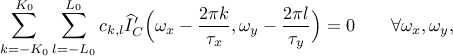
wher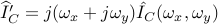e . We show that it is possible to reconstruct the parameters of the curve (i.e. to detect the exact edge positions in the continuous domain) based on the annihilation equations from a few samples of the edge image 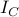(e.g., Figure 1).

Figure 1: From left to right: The original edge image 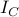; Samples of the edge image (size: 9 by 9); Reconstructed FRI curve from the samples.

Moreover, the annihilation equations that characterize the curve are linear constraints that can be easily exploited in optimization problems for further image processing (e.g., image up-sampling). We demonstrate one potential application of the annihilation algorithm with examples in edge-preserving interpolation.

Experimental results with both synthetic curves as well as edges of natural images clearly show the effectiveness of the annihilation constraint in preserving sharp edges, and improving SNRs (e.g., Figure 2).

Figure 2: From left to right: The given low-resolution image (size: 85 by 85); Up-sampled image without annihilation constraint (size: 255 by 255, PSNR = 29.62dB); Up-sampled image with annihilation constraint (size: 255 by 255, PSNR = 30.89dB).

References

[1] Pan, H., Blu, T. & Dragotti, P.-L.,"Sampling Curves with Finite Rate of Innovation", IEEE Transactions on Signal Processing, 2013.

[2] Pan, H., Blu, T. & Dragotti, P.-L.,"Sampling Curves with Finite Rate of Innovation", Proceedings of the Ninth International Workshop on Sampling Theory and Applications (SampTA'11), Singapore, May 2--6, 2011.